Actinide-Boost Stars may not
Suggest a Separate r-Process Site

Erika M. Holmbeck

28 March 2019

r-process enhanced stars

from data in McWilliam+ (1995), Sneden+ (2003)

Uranium in RAVE J203843.2-002333

Placco, Holmbeck+ (2017)

Uranium in J0954+5246

Holmbeck+ (2018)

The actinide boost and J0954+5246

Holmbeck+ (2018)

Ages and cosmochronometry

Holmbeck+ (2018)

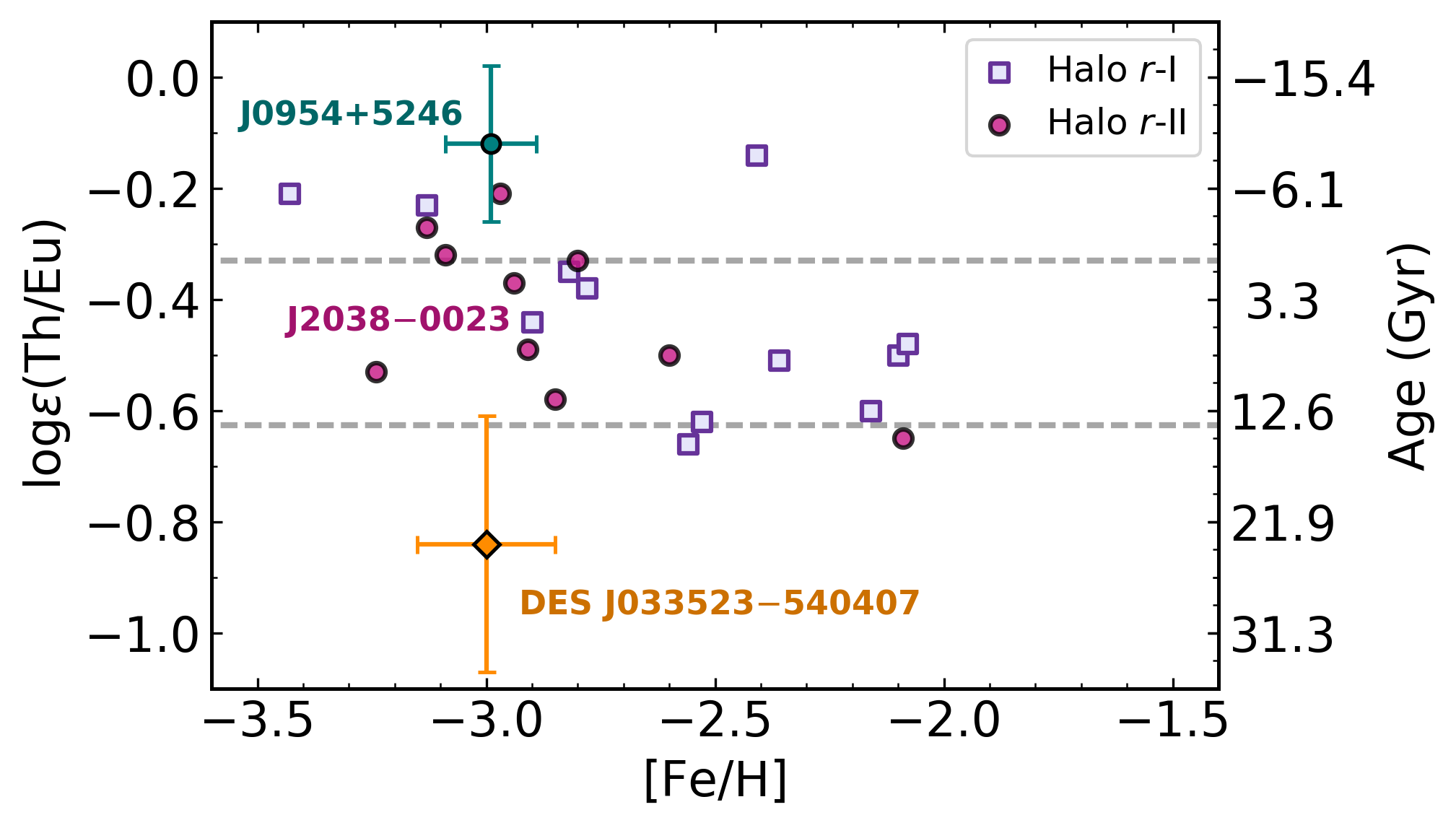
Ages and cosmochronometry

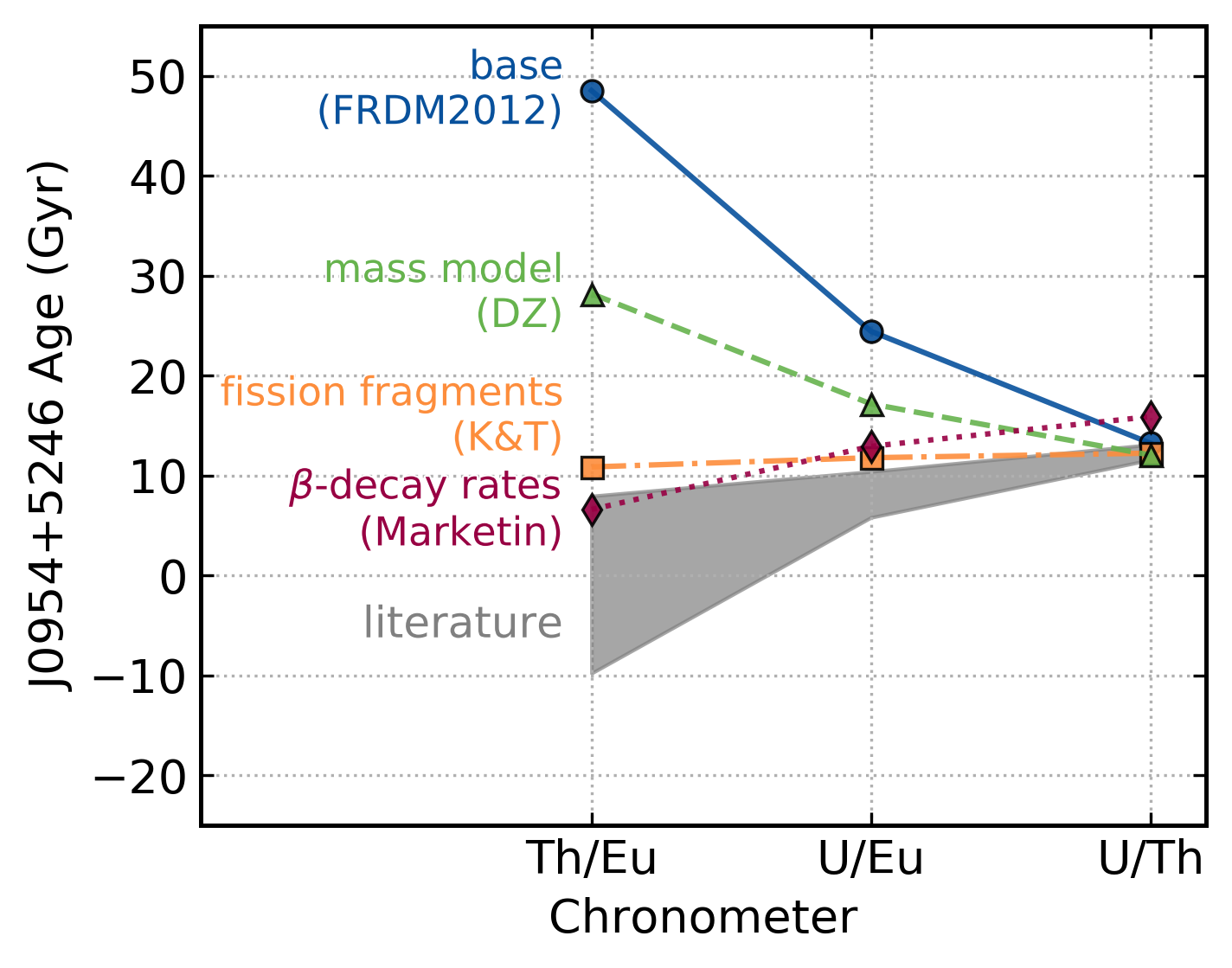
232-Th and 238-U are radioactive

Allows radioactive decay dating

$$ t = 46.67~\text{Gyr} \left[\log\epsilon\left(\text{Th/Eu}\right)_0 - \log\epsilon\left(\text{Th/Eu}\right)_{\text{obs}}\right] $$
$$ t = 14.84~\text{Gyr} \left[\log\epsilon\left(\text{U/Eu}\right)_0 - \log\epsilon\left(\text{U/Eu}\right)_{\text{obs}}\right] $$
$$ t = 21.80~\text{Gyr} \left[\log\epsilon\left(\text{U/Th}\right)_0 - \log\epsilon\left(\text{U/Th}\right)_{\text{obs}}\right] $$

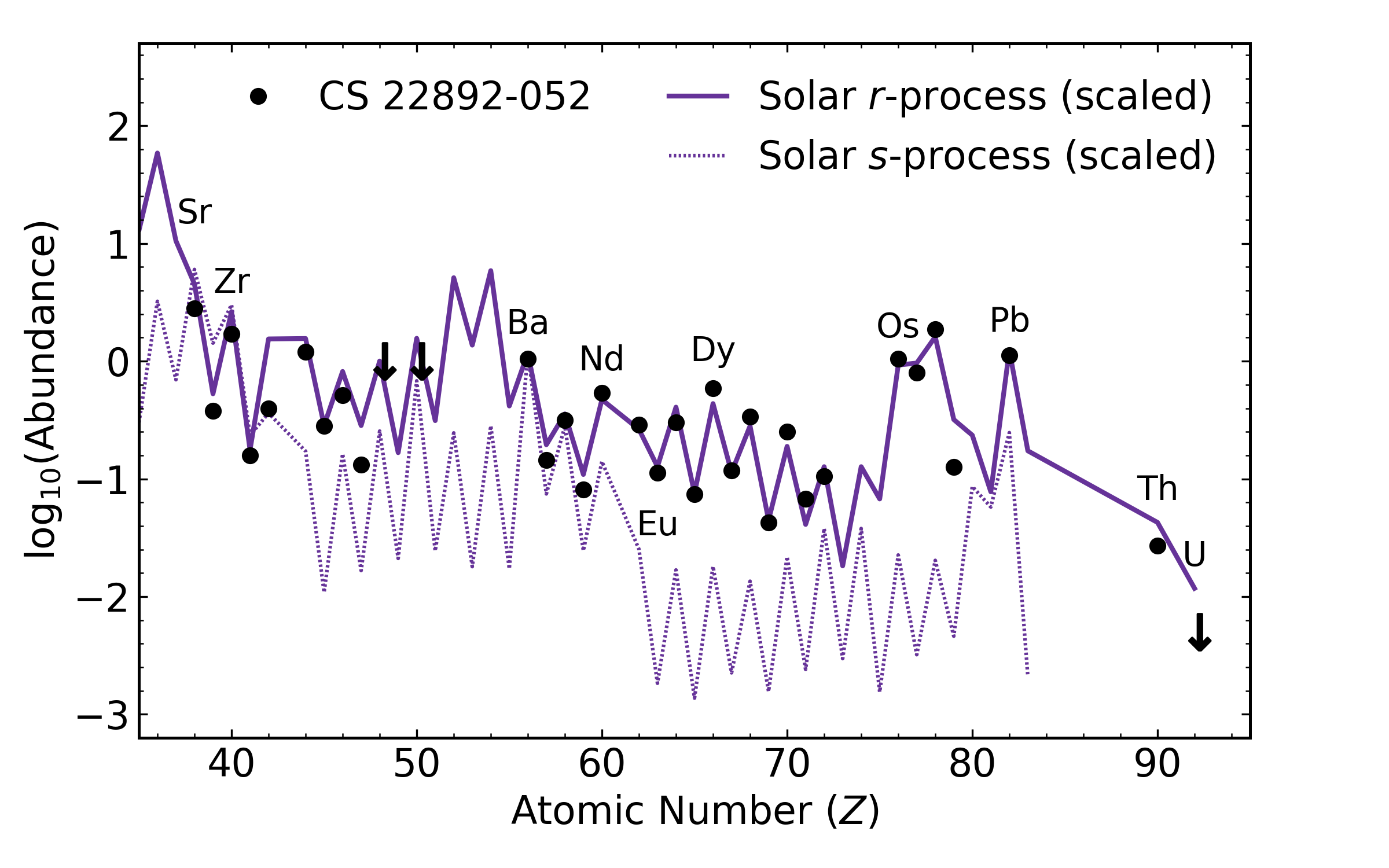
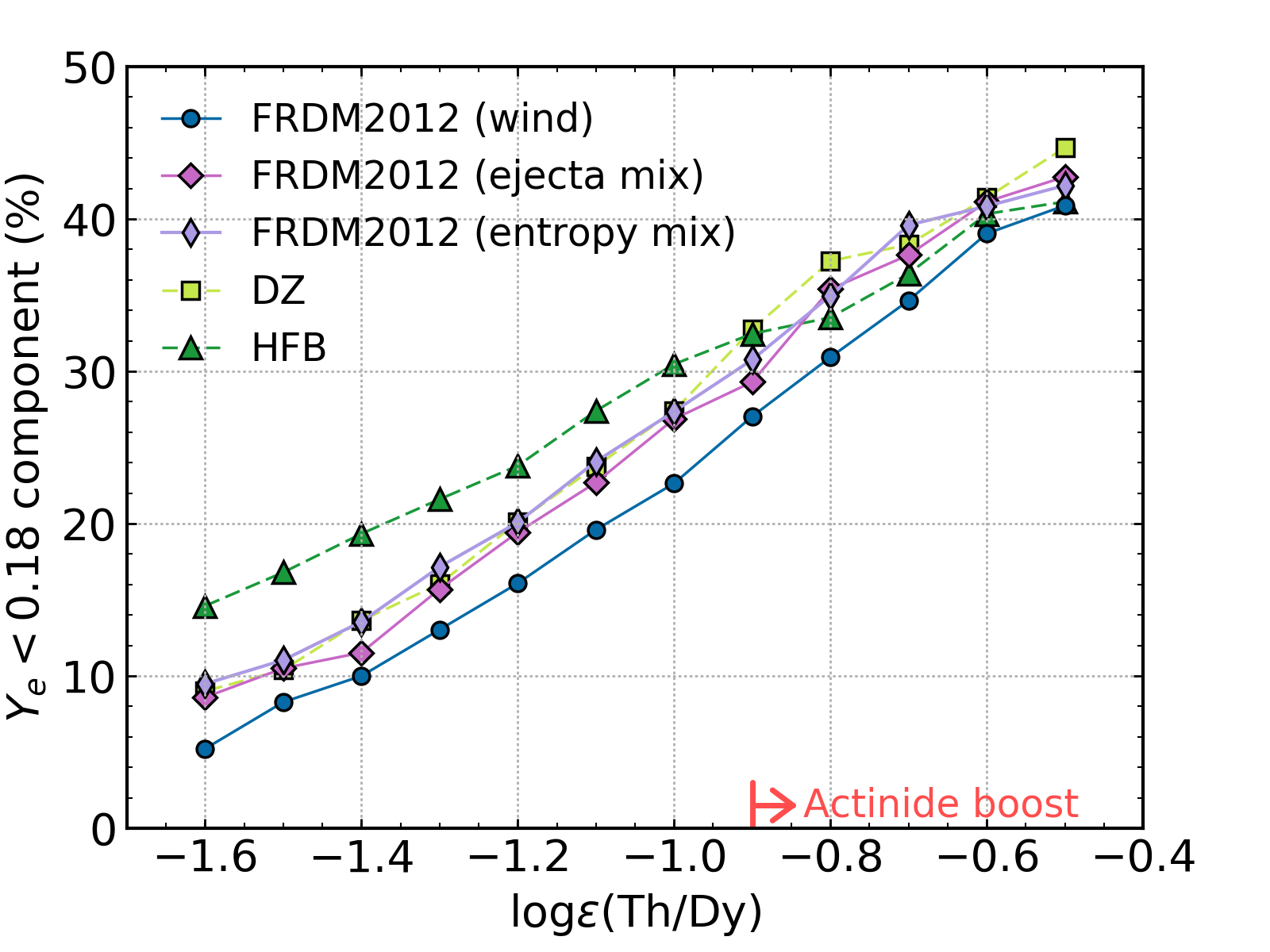
Actinides and the r-process

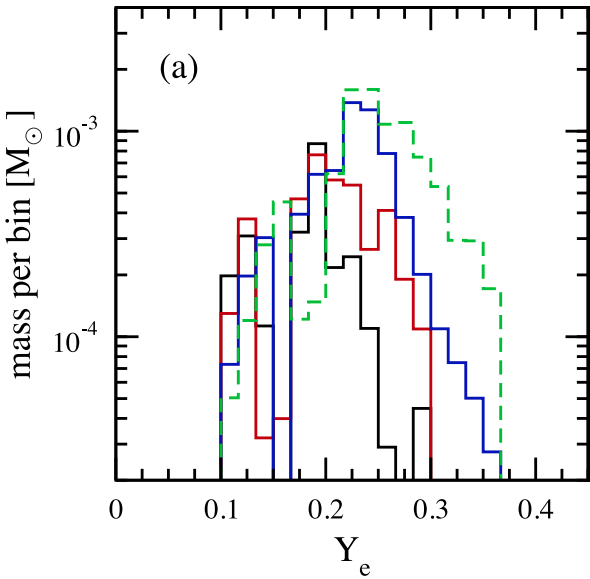
Can varying levels of neutron richness
in a NSM account for the actinide boost?

M. Mumpower and T. Sprouse

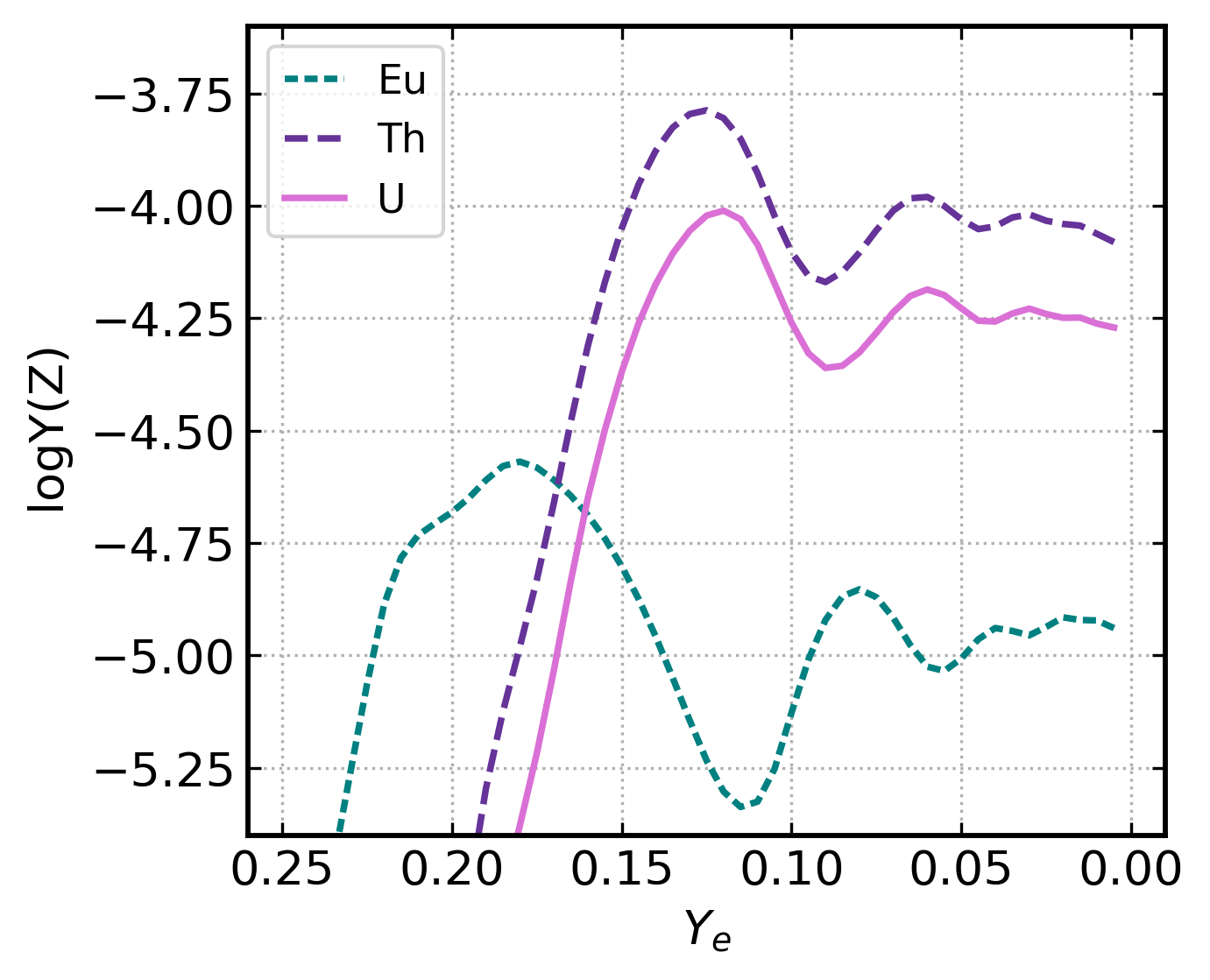
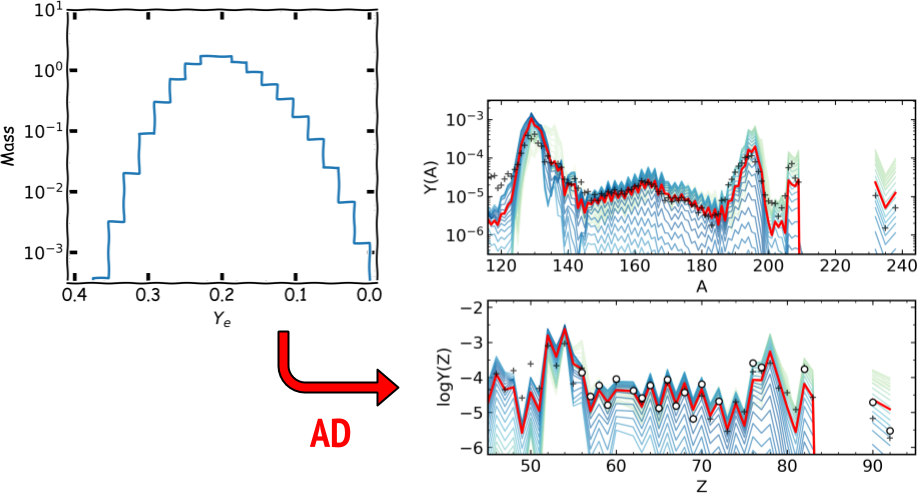
Low-entropy dynamical (tidal) ejecta of a NSM
(Korobkin+ 2012; Rosswog+ 2013)

Vary the initial electron fraction: $Y_e=0.005 - 0.250$

---

$Y_e = \left[1+(n/p)\right]^{-1}$

Actinide and lanthanide production

Holmbeck with PRISM (T. Sprouse and M. Mumpower)

Actinide and lanthanide production

Holmbeck+ (2019)

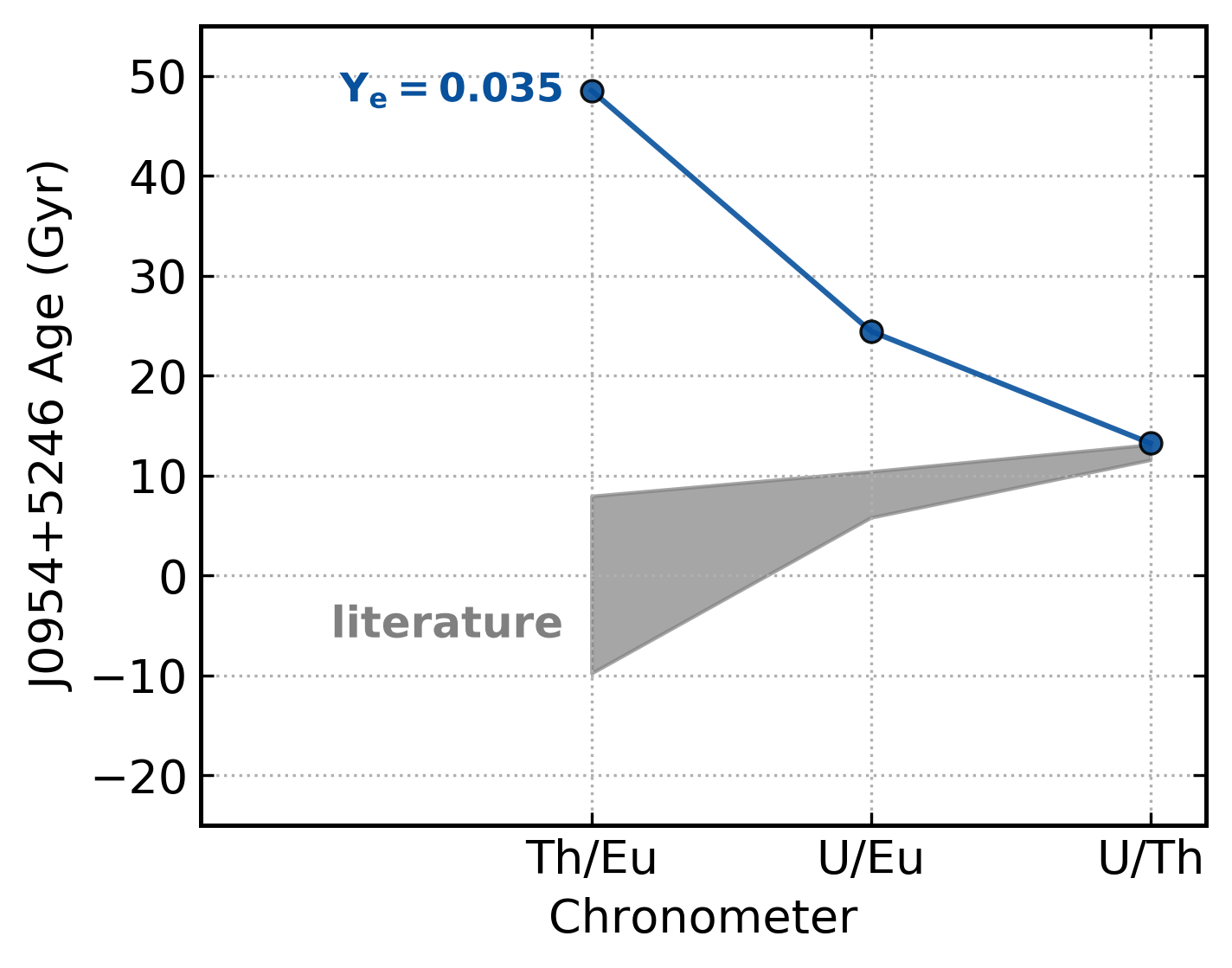
Ages and cosmochronometry

$$ t = 46.67~\text{Gyr} \left[\log\epsilon\left(\text{Th/Eu}\right)_0 - \log\epsilon\left(\text{Th/Eu}\right)_{\text{obs}}\right] $$
$$ t = 14.84~\text{Gyr} \left[\log\epsilon\left(\text{U/Eu}\right)_0 - \log\epsilon\left(\text{U/Eu}\right)_{\text{obs}}\right] $$
$$ t = 21.80~\text{Gyr} \left[\log\epsilon\left(\text{U/Th}\right)_0 - \log\epsilon\left(\text{U/Th}\right)_{\text{obs}}\right] $$

The age of J0954+5246

Holmbeck+ (2019)

Nuclear physics variations

from data in Holmbeck+ (2019)

The age of J0954+5246

Holmbeck+ (2019)

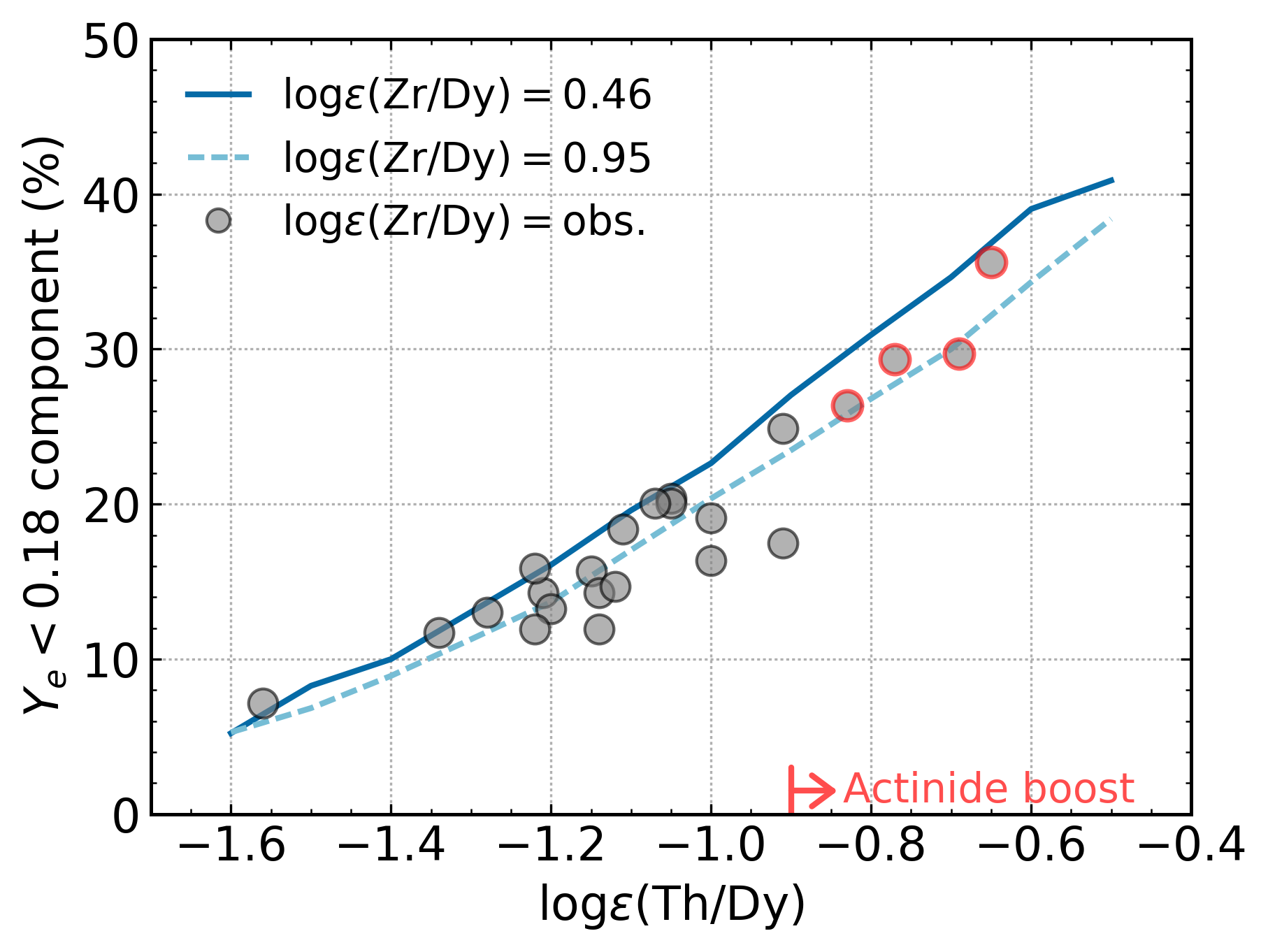
Actinides are currently not observed
at such high levels

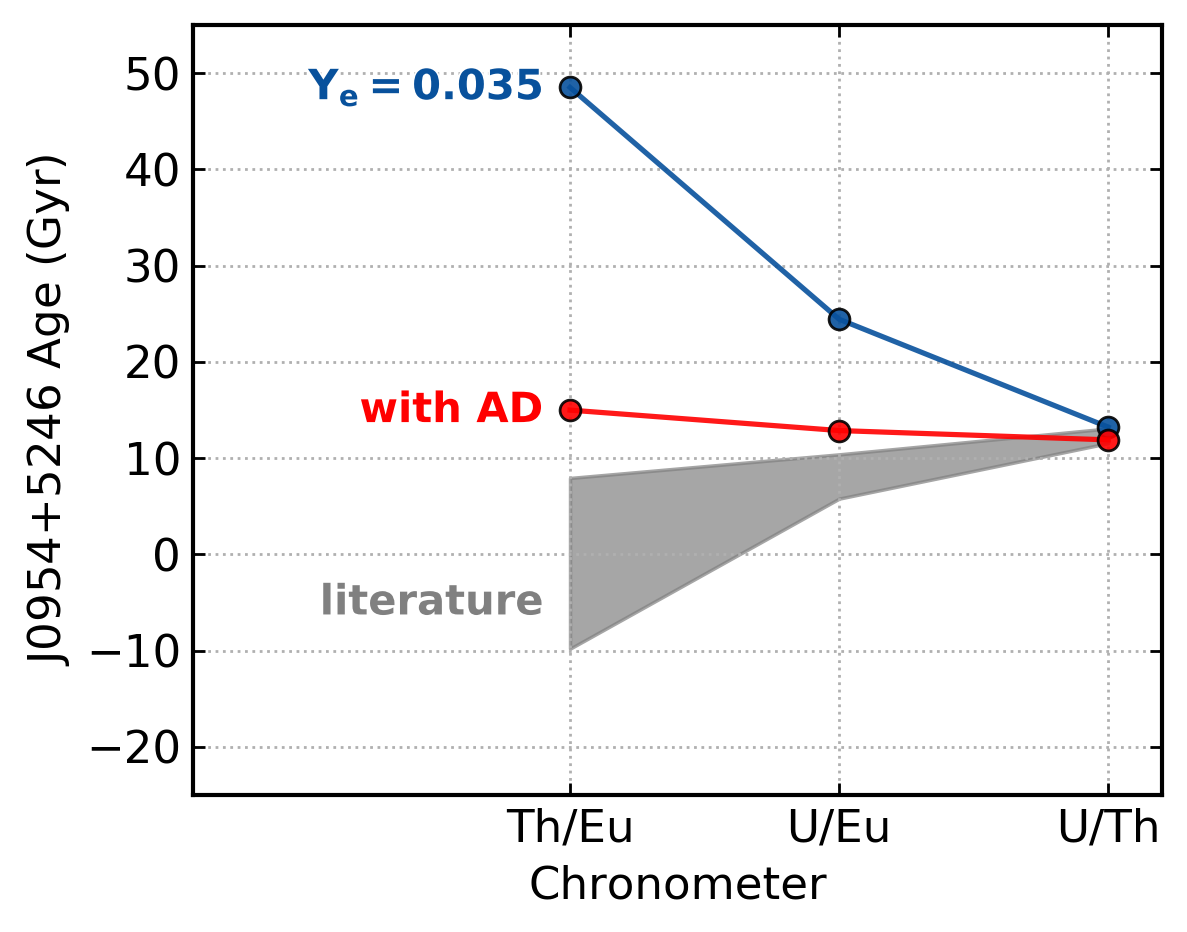
Need a method to dilute the actinides to reduce the Th/Eu production ratio

Actinide-Dilution model

Distribution of $Y_e$

Tidal ejecta
($Y_e\approx 0.16$, Bovard+ 2017)

Disk wind
($Y_e\approx 0.22$; Lippuner+ 2017)

$m_{\rm wind}/m_{\rm dyn}= 3$
from estimates of GW170817
(Rosswog+ 2017; Tanaka+ 2017)

Actinide-Dilution model

Holmbeck+ (2019)

Ages

Holmbeck+ (2019)

Ages

Holmbeck+ (2019)

AD Model

Can we go backwards?

Reticulum II

Ji+ (2016)

Groups of r-process enhanced stars

Holmbeck+ (in prep. 2019)

Assume one event

that produces the entire r-process pattern

Not necessarily an NSM

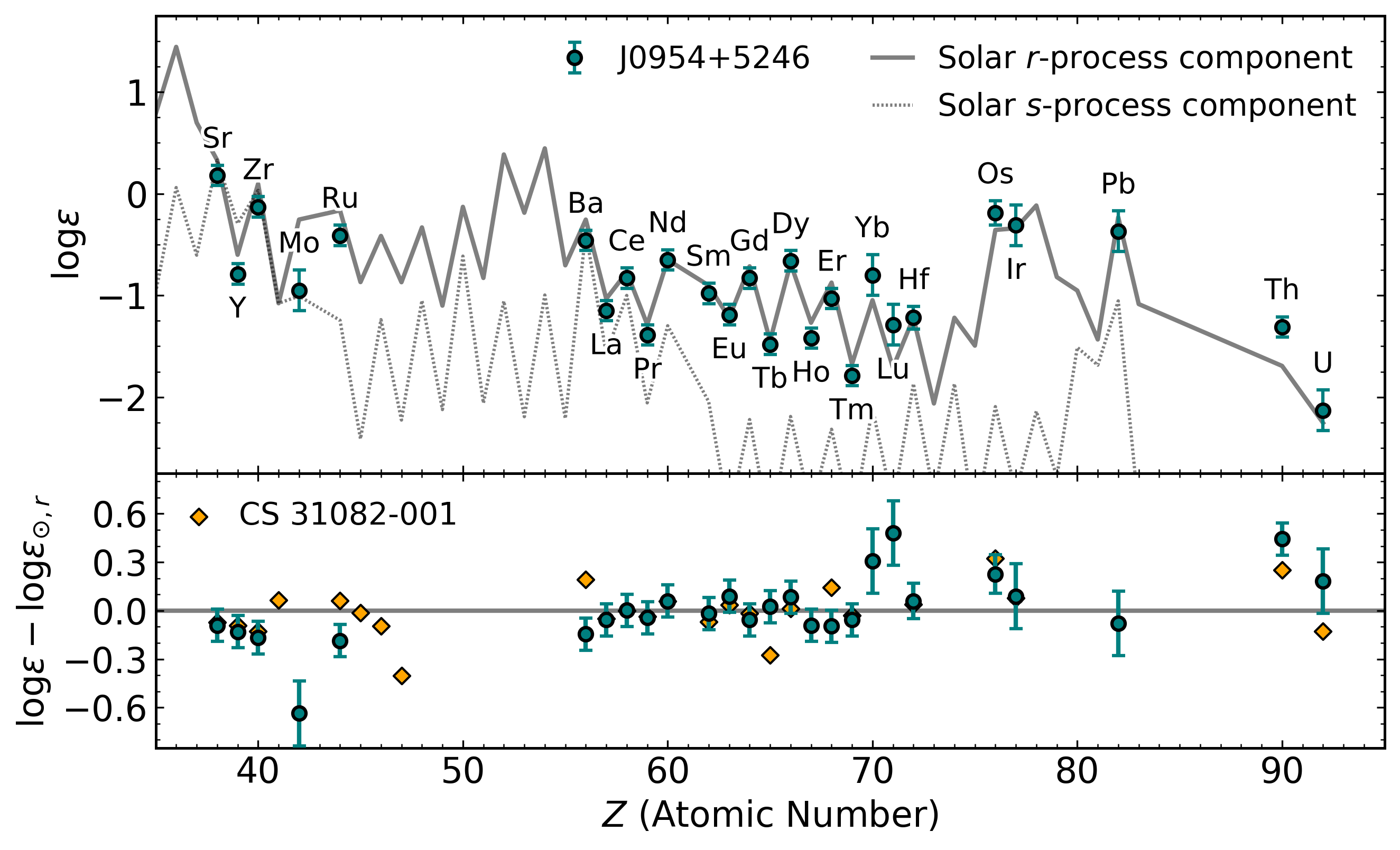
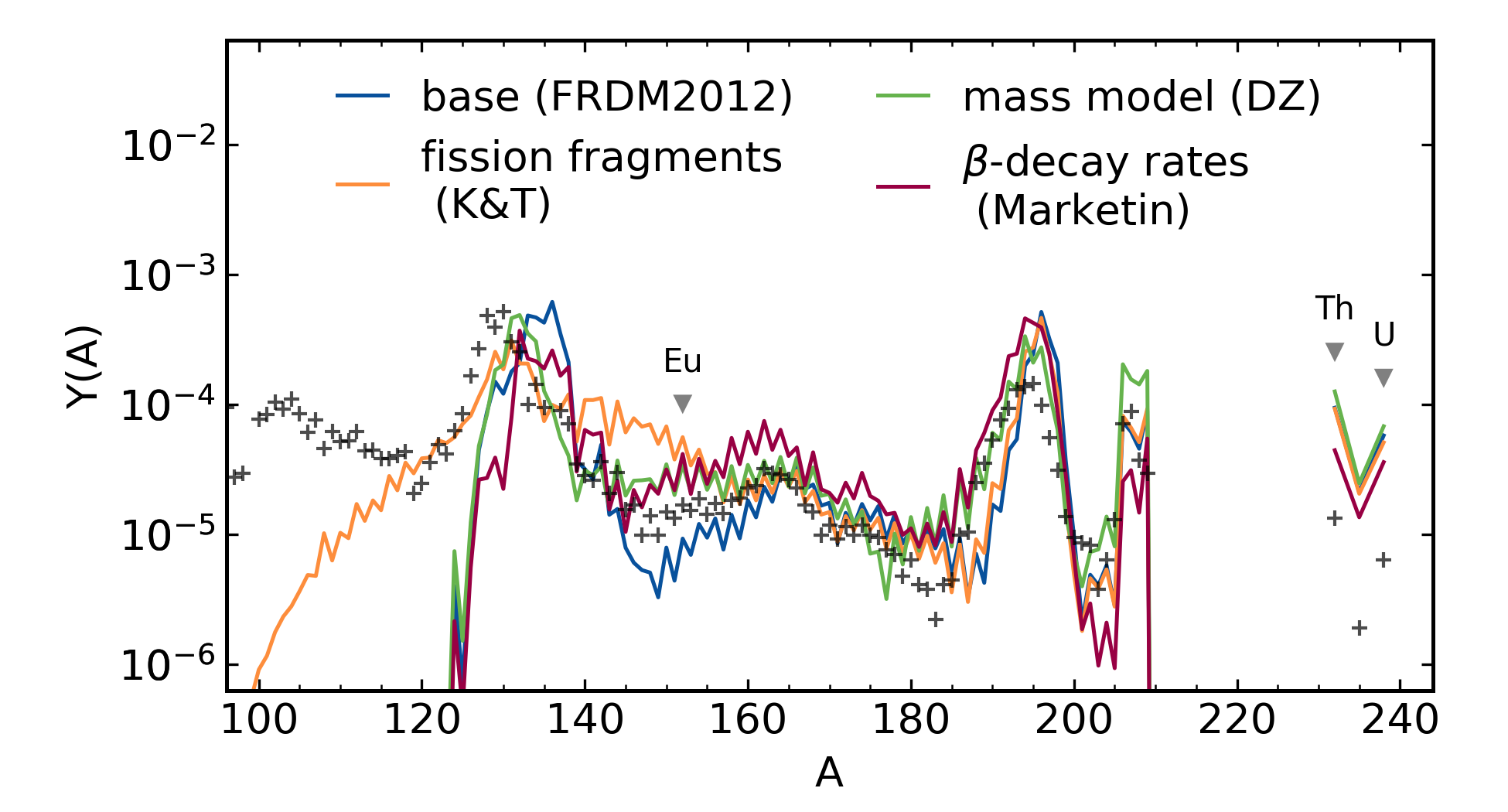
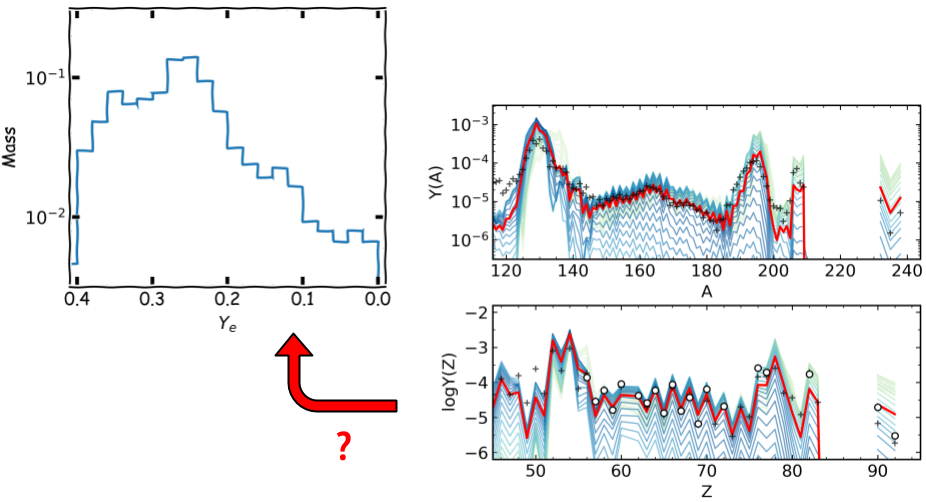
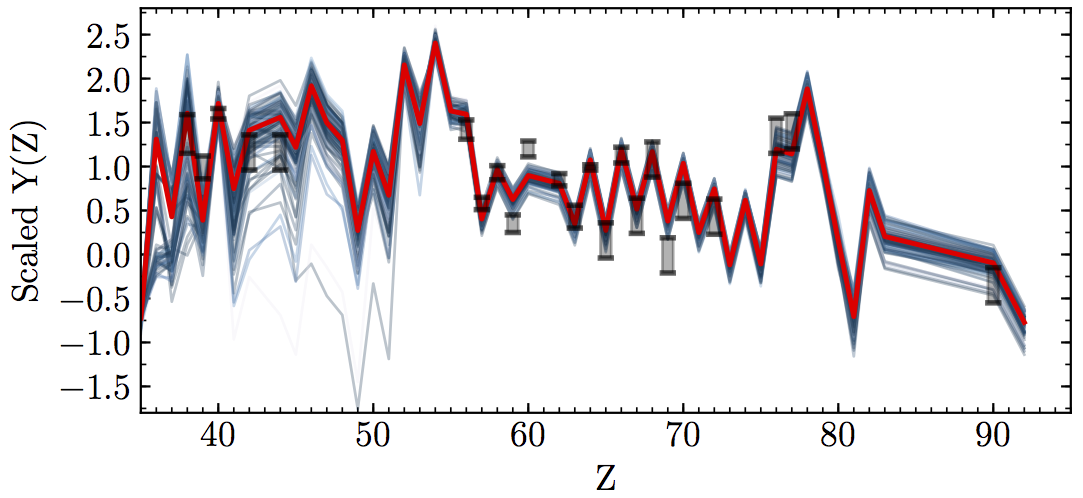
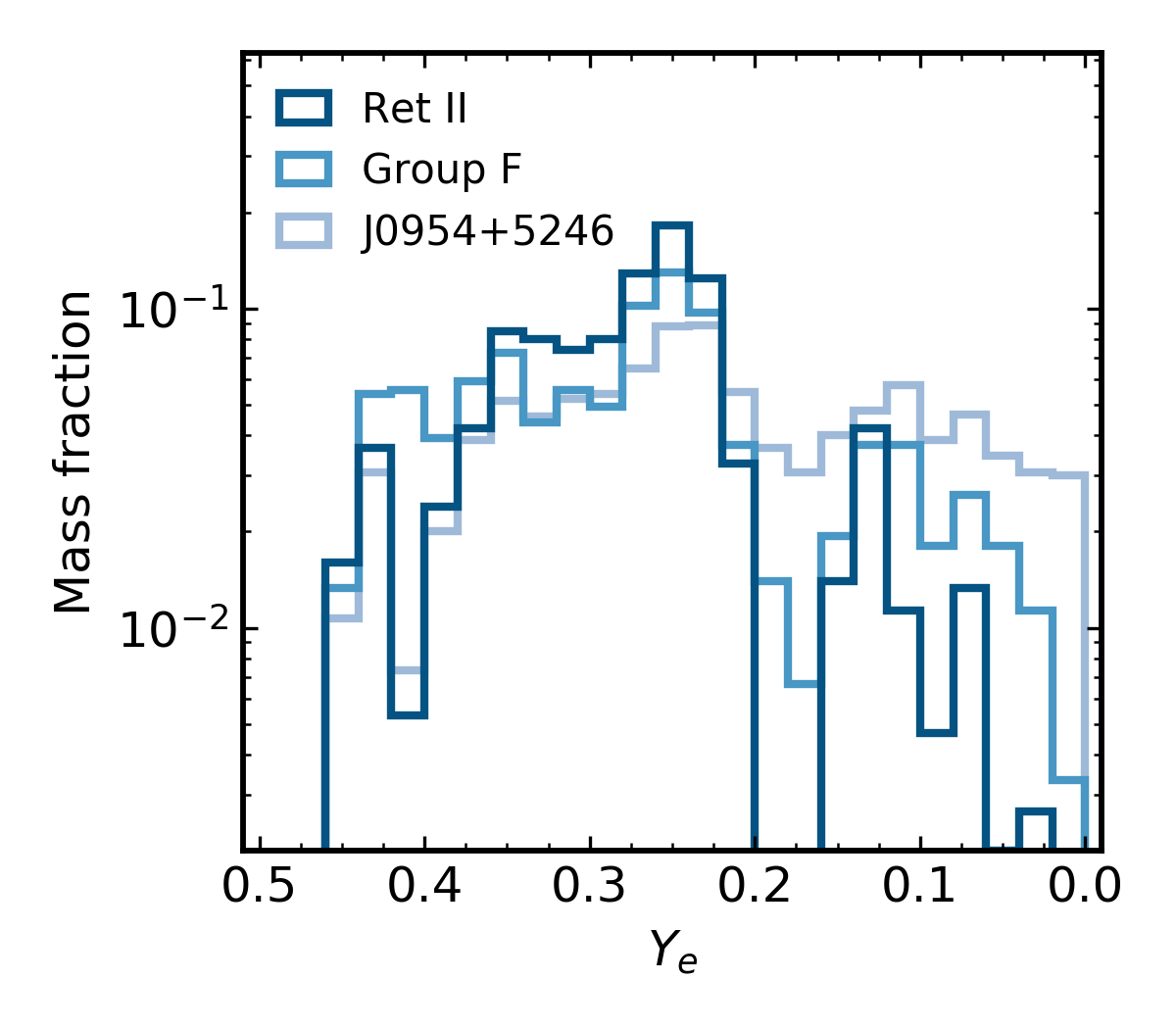
Actinide-Dilution with Matching model

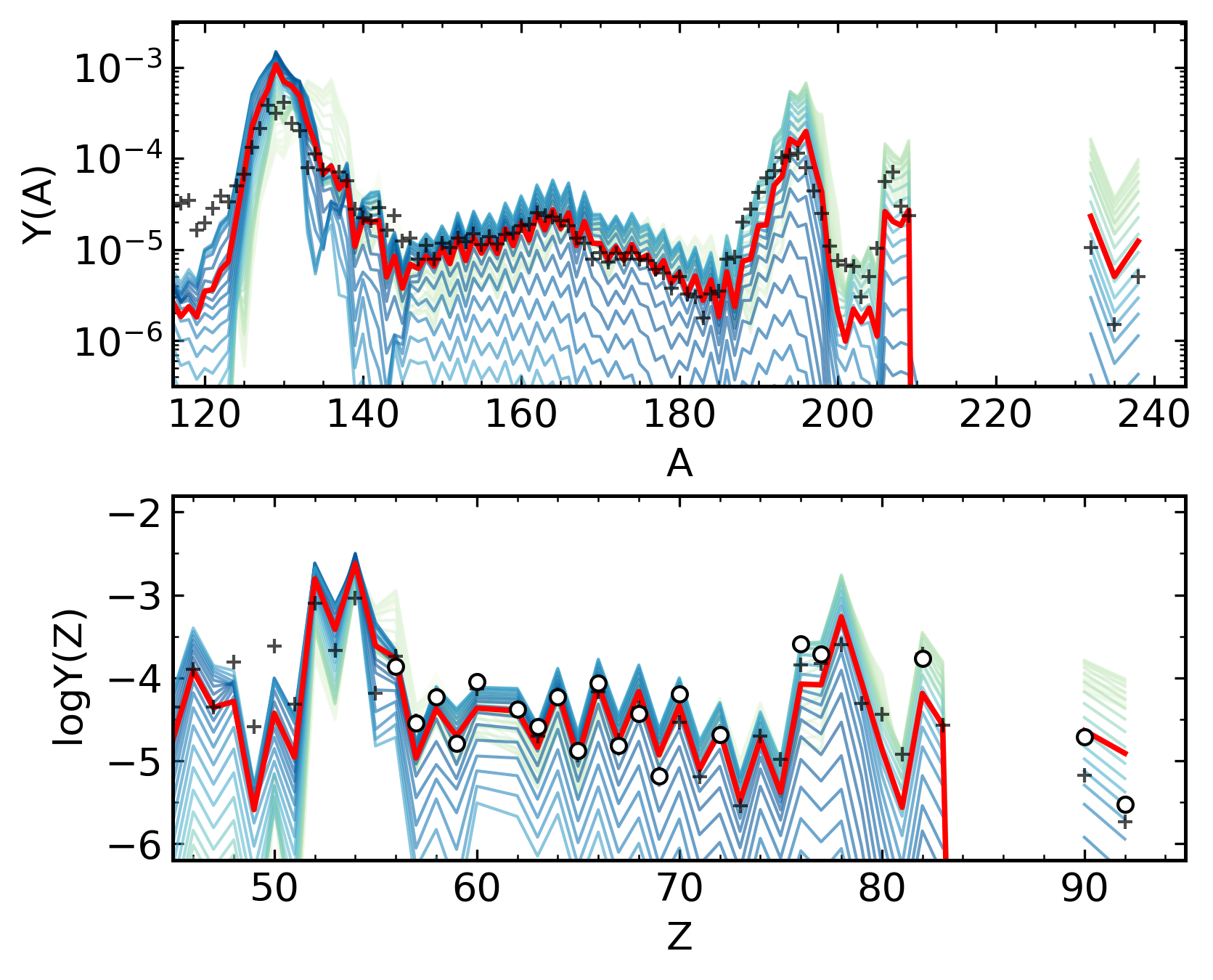
Builds empircal mass ejecta distributions as a function of $Y_e$ (0.005-0.450)

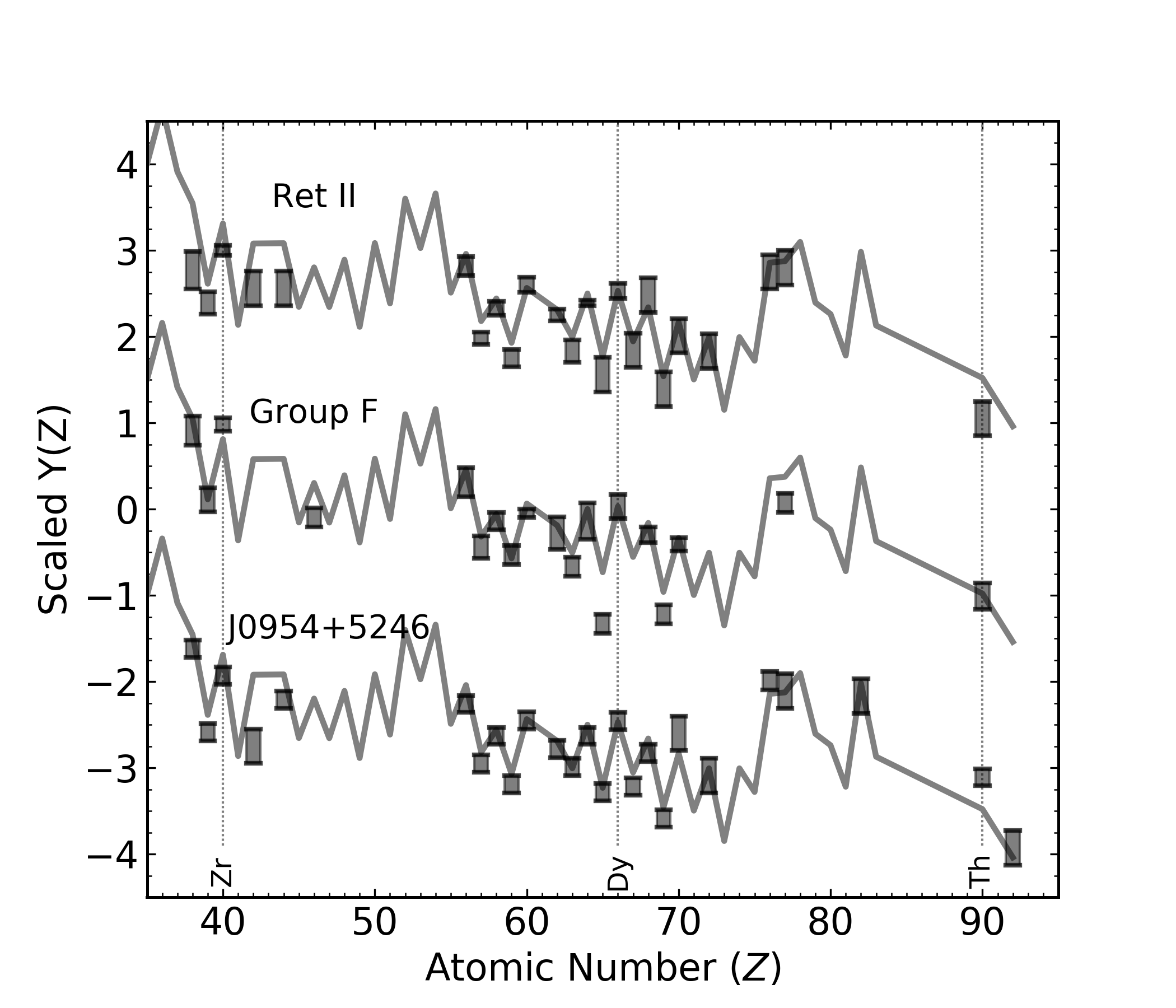
To explain entire pattern from Zr to U

ADM abundance pattern for Ret II

Holmbeck+ (in prep. 2019)

Empirically built ejecta mass distributions

Holmbeck+ (in prep. 2019)

NSM ejecta (literature)

Fernandez+ (2015)

The low-Ye component

Holmbeck+ (in prep. 2019)

Low-Ye component under variations

Holmbeck+ (in prep. 2019)

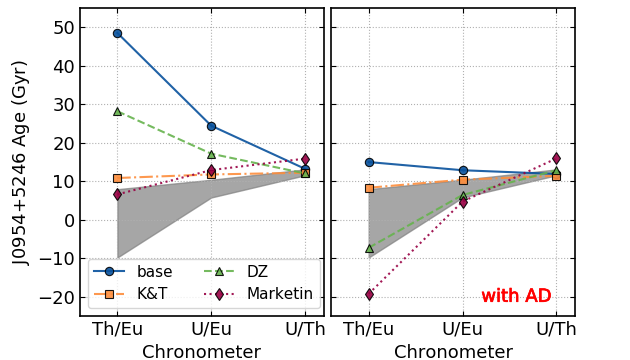
Actinide-boost stars do not call for
a separate r-process progenitor

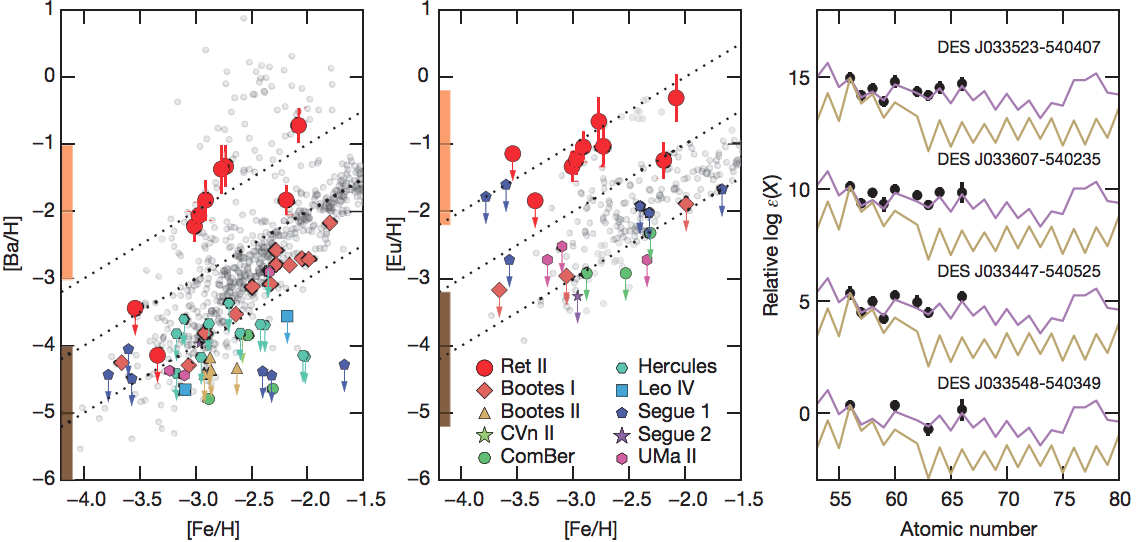
Is this source an NSM?

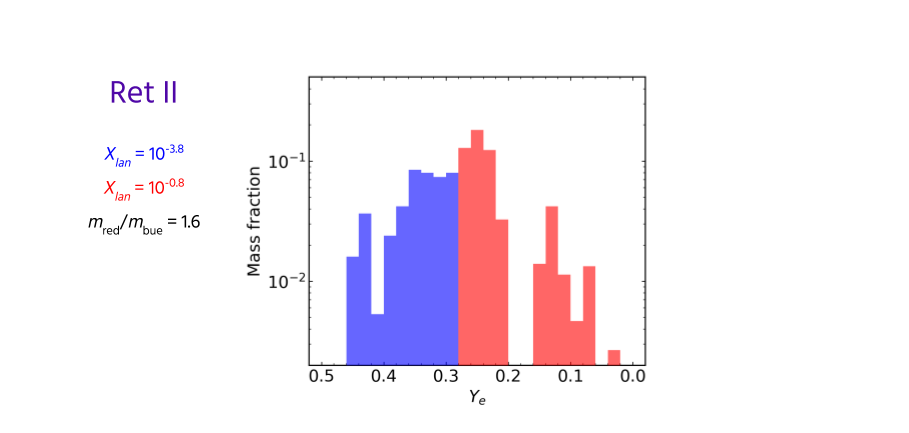
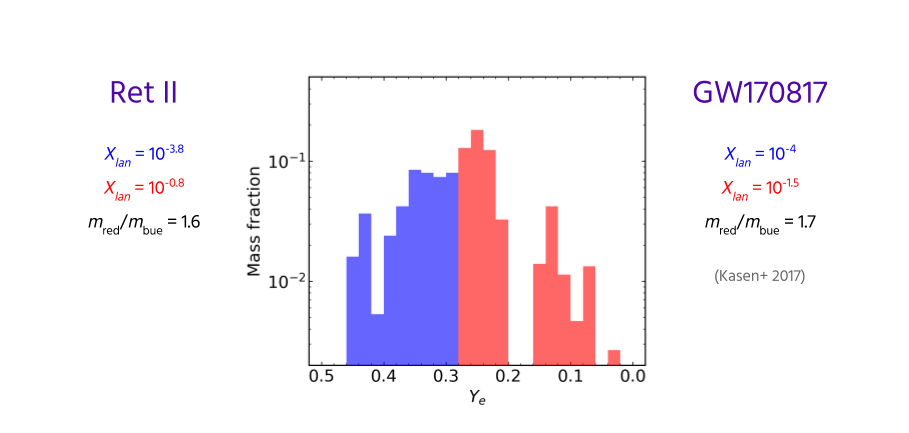
Results derived from r-II stars
agree* with NSM observation

Summary and Outlook

The actinides are over-produced in very cold, neutron-rich (tidal) ejecta

NSMs could still be an actinide-boost source if most of the ejecta mass does not contribute actinides

The same r-process source can in principle account for observed actinide variations

How do the empirically built ejecta distributions compare to NSM simulations?

Entropy, dynamical timescale, nuclear physics variations...

Special Thanks

Rebecca Surman (ND), Nicole Vassh (ND), Matthew Mumpower (LANL), Trevor M. Sprouse (ND)
Gail C. McLaughlin (NC State), Anna Frebel (MIT)

Timothy C. Beers (ND), Terese T. Hansen (TAMU), Chris Sneden (UT-Austin), Vinicius M. Placco (ND),
Ian U. Roederer (UMich.), Charli M. Sakari (UW), Rana Ezzeddine (MIT)
Grant Mathews (ND), Ani Aprahamian (ND), Toshihiko Kawano (LANL)